Анализ данных с помощью Python

В этой статье мы обсудим, как выполнять анализ данных с помощью Python. Мы обсудим все виды анализа данных, т.е. анализ числовых данных с помощью NumPy, табличных данных с помощью Pandas, визуализацию данных Matplotlib и исследовательский анализ данных.

Анализ данных с помощью Python

Анализ данных - это метод сбора, преобразования и организации данных для прогнозирования будущего и принятия обоснованных решений на основе данных. Это также помогает находить возможные решения бизнес-задач. Для анализа данных существует шесть шагов. Это:

• Спросите или укажите требования к данным
• Подготовка или сбор данных
• Очистка и обработка
• Анализировать
• Поделиться
• Действовать или сообщать

Анализ числовых данных с помощью NumPy

NumPy - это пакет обработки массивов на Python, предоставляющий высокопроизводительный объект многомерного массива и инструменты для работы с этими массивами. Это фундаментальный пакет для научных вычислений с использованием Python.

Массивы в NumPy

Массив NumPy представляет собой таблицу элементов (обычно чисел), все одного и того же типа, проиндексированную набором положительных целых чисел. В Numpy количество измерений массива называется рангом массива. Набор целых чисел, задающих размер массива по каждому измерению, известен как форма массива.

Создание массива NumPy

Массивы NumPy могут быть созданы несколькими способами с различными рангами. Он также может быть создан с использованием различных типов данных, таких как списки, кортежи и т.д. Тип результирующего массива определяется по типу элементов в последовательностях. NumPy предлагает несколько функций для создания массивов с исходным содержимым-заполнителем. Они сводят к минимуму необходимость увеличения массивов, что является дорогостоящей операцией.

Создайте массив с помощью numpy.empty(shape, dtype=float, order=’C’)

import numpy as np
 
b = np.empty(2, dtype = int)
print("Matrix b : \n", b)
 
a = np.empty([2, 2], dtype = int)
print("\nMatrix a : \n", a)
 
c = np.empty([3, 3])
print("\nMatrix c : \n", c)

Вывод:

Matrix b : 
 [1065353216 1065353216]

Matrix a : 
 [[-1253146667 -1065797382]
 [   19889362   322685255]]

Matrix c : 
 [[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]

Создайте массив, используя numpy.zeros(shape, dtype = None, order = ‘C’)

import numpy as np
 
b = np.zeros(2, dtype = int)
print("Matrix b : \n", b)
 
a = np.zeros([2, 2], dtype = int)
print("\nMatrix a : \n", a)
 
c = np.zeros([3, 3])
print("\nMatrix c : \n", c)

Вывод:

Matrix b : 
 [0 0]

Matrix a : 
 [[0 0]
 [0 0]]

Matrix c : 
 [[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]

Операции с массивами Numpy

Арифметические операции

• Дополнение:

import numpy as np

# Defining both the matrices
a = np.array([5, 72, 13, 100])
b = np.array([2, 5, 10, 30])

# Performing addition using arithmetic operator
add_ans = a+b
print(add_ans)

# Performing addition using numpy function
add_ans = np.add(a, b)
print(add_ans)

# The same functions and operations can be used for
# multiple matrices
c = np.array([1, 2, 3, 4])
add_ans = a+b+c
print(add_ans)

add_ans = np.add(a, b, c)
print(add_ans)

Вывод:

[  7  77  23 130]
[  7  77  23 130]
[  8  79  26 134]
[  7  77  23 130]

• Вычитание:

import numpy as np

# Defining both the matrices
a = np.array([5, 72, 13, 100])
b = np.array([2, 5, 10, 30])

# Performing subtraction using arithmetic operator
sub_ans = a-b
print(sub_ans)

# Performing subtraction using numpy function
sub_ans = np.subtract(a, b)
print(sub_ans)

Вывод:

[ 3 67  3 70]
[ 3 67  3 70]

• Умножение:

import numpy as np

# Defining both the matrices
a = np.array([5, 72, 13, 100])
b = np.array([2, 5, 10, 30])

# Performing multiplication using arithmetic
# operator
mul_ans = a*b
print(mul_ans)

# Performing multiplication using numpy function
mul_ans = np.multiply(a, b)
print(mul_ans)

Вывод:

[  10  360  130 3000]
[  10  360  130 3000]

• Подразделение:

import numpy as np

# Defining both the matrices
a = np.array([5, 72, 13, 100])
b = np.array([2, 5, 10, 30])

# Performing division using arithmetic operators
div_ans = a/b
print(div_ans)

# Performing division using numpy functions
div_ans = np.divide(a, b)
print(div_ans)

Вывод:

[ 2.5        14.4         1.3         3.33333333]
[ 2.5        14.4         1.3         3.33333333]

Индексирование массива NumPy

Индексацию можно выполнить в NumPy, используя массив в качестве индекса. В случае среза возвращается видовая или поверхностная копия массива, но в индексном массиве возвращается копия исходного массива. Массивы Numpy могут быть проиндексированы вместе с другими массивами или любой другой последовательностью, за исключением кортежей. Последний элемент индексируется на -1, предпоследний на -2 и так далее.

Индексирование массива Python NumPy

# Python program to demonstrate 
# the use of index arrays.
import numpy as np
 
# Create a sequence of integers from
# 10 to 1 with a step of -2
a = np.arange(10, 1, -2) 
print("\n A sequential array with a negative step: \n",a)
 
# Indexes are specified inside the np.array method.
newarr = a[np.array([3, 1, 2 ])]
print("\n Elements at these indices are:\n",newarr)

Вывод:

A sequential array with a negative step: 
 [10  8  6  4  2]

 Elements at these indices are:
 [4 8 6]

Нарезка массива NumPy

Рассмотрим синтаксис x[obj], где x — это массив, а obj — индекс. Объект среза является индексом в случае базового среза. Базовый срез происходит, когда obj равно :

• объект среза, имеющий вид start: stop: step
• целое число
• или набор объектов slice и целых чисел

Все массивы, созданные с помощью базовой нарезки, всегда являются представлением исходного массива.

# Python program for basic slicing.
import numpy as np

# Arrange elements from 0 to 19
a = np.arange(20)
print("\n Array is:\n ",a)

# a[start:stop:step]
print("\n a[-8:17:1] = ",a[-8:17:1])

# The : operator means all elements till the end.
print("\n a[10:] = ",a[10:])

Вывод:

Array is:
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19]

a[-8:17:1]  =  [12 13 14 15 16]

a[10:] = [10 11 12 13 14 15 16 17 18 19]

Многоточие также можно использовать вместе с базовым разделением. Многоточие (...) - это количество : объектов, 
необходимых для создания кортежа выборки той же длины, что и размеры массива.

# Python program for indexing using basic slicing with ellipsis
import numpy as np

# A 3 dimensional array.
b = np.array([[[1, 2, 3],[4, 5, 6]],
            [[7, 8, 9],[10, 11, 12]]])

print(b[...,1]) #Equivalent to b[: ,: ,1 ]

Вывод:

[[ 2  5]
 [ 8 11]]

Трансляция массива NumPy

Термин «расширение» относится к тому, как NumPy обрабатывает массивы с разными размерами во время арифметических операций, что приводит к определённым ограничениям. Меньший массив расширяется за счёт большего массива, чтобы они имели совместимые формы.

Предположим, что у нас есть большой набор данных, где каждая запись представляет собой список параметров. В Numpy у нас есть двумерный массив, где каждая строка — это запись, а количество строк — это размер набора данных. Предположим, что мы хотим применить какое-то масштабирование ко всем этим данным, чтобы каждый параметр получил свой собственный коэффициент масштабирования или, скажем, чтобы каждый параметр был умножен на какой-то коэффициент.

Просто чтобы иметь четкое представление, давайте посчитаем калории в продуктах, используя разбивку по макроэлементам. Грубо говоря, калорийность пищи состоит из жиров (9 калорий на грамм), белков (4 калорийных грамма) и углеводов (4 калорийных грамма). Итак, если мы перечислим некоторые продукты (наши данные) и для каждого продукта перечислим его распределение по макронутриентам (параметры), мы можем затем умножить каждое питательное вещество на его калорийность (применить масштабирование), чтобы вычислить калорийность каждого продукта.

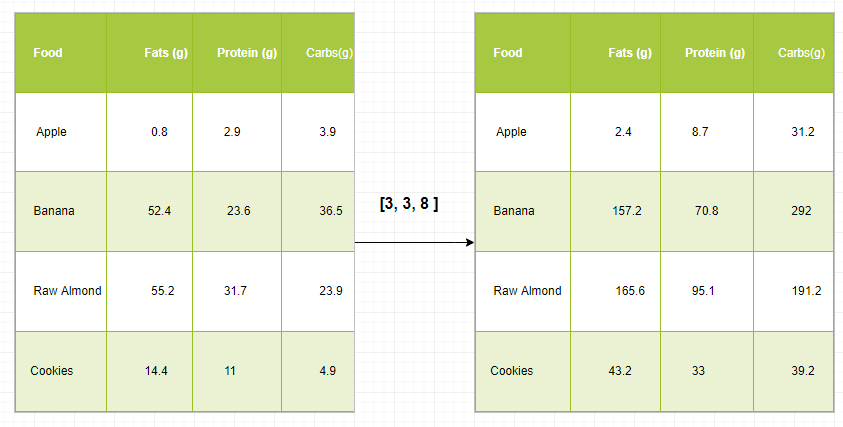
С помощью этого преобразования мы теперь можем вычислять любую полезную информацию. Например, сколько калорий содержится в каком-либо продукте или, зная состав моего ужина, сколько калорий я получил из белка и так далее.

Давайте посмотрим на наивный способ произвести это вычисление с помощью Numpy:

import numpy as np

macros = np.array([
[0.8, 2.9, 3.9],
[52.4, 23.6, 36.5],
[55.2, 31.7, 23.9],
[14.4, 11, 4.9]
])

# Create a new array filled with zeros,
# of the same shape as macros.
result = np.zeros_like(macros)

cal_per_macro = np.array([3, 3, 8])

# Now multiply each row of macros by
# cal_per_macro. In Numpy, `*` is
# element-wise multiplication between two arrays.
for i in range(macros.shape[0]):
    result[i, :] = macros[i, :] * cal_per_macro

result

Вывод:

array([[  2.4,   8.7,  31.2],
       [157.2,  70.8, 292. ],
       [165.6,  95.1, 191.2],
       [ 43.2,  33. ,  39.2]])

Правила трансляции: Объедините два массива вместе, следуя этим правилам:

• Если массивы не имеют одинакового ранга, то добавляйте перед формой массива более низкого ранга 1s, пока обе формы не будут иметь одинаковую длину.
• Два массива совместимы по одному измерению, если они имеют одинаковый размер по этому измерению или если один из массивов имеет размер 1 по этому измерению.
• Массивы могут транслироваться вместе, если они совместимы со всеми измерениями.
• После трансляции каждый массив ведёт себя так, как если бы его форма была равна максимальному значению из форм двух входных массивов.
• В любом измерении, где один массив имеет размер 1, а другой массив имеет размер больше 1, первый массив ведёт себя так, как если бы он был скопирован в этом измерении.

import numpy as np

v = np.array([12, 24, 36])
w = np.array([45, 55])

# To compute an outer product we first
# reshape v to a column vector of shape 3x1
# then broadcast it against w to yield an output
# of shape 3x2 which is the outer product of v and w
print(np.reshape(v, (3, 1)) * w)

X = np.array([[12, 22, 33], [45, 55, 66]])

# x has shape 2x3 and v has shape (3, )
# so they broadcast to 2x3,
print(X + v)

# Add a vector to each column of a matrix X has
# shape 2x3 and w has shape (2, ) If we transpose X
# then it has shape 3x2 and can be broadcast against w
# to yield a result of shape 3x2.

# Transposing this yields the final result
# of shape 2x3 which is the matrix.
print((X.T + w).T)

# Another solution is to reshape w to be a column
# vector of shape 2X1 we can then broadcast it
# directly against X to produce the same output.
print(X + np.reshape(w, (2, 1)))

# Multiply a matrix by a constant, X has shape 2x3.
# Numpy treats scalars as arrays of shape();
# these can be broadcast together to shape 2x3.
print(X * 2)

Вывод:

[[ 540  660]
 [1080 1320]
 [1620 1980]]
[[ 24  46  69]
 [ 57  79 102]]
[[ 57  67  78]
 [100 110 121]]
[[ 57  67  78]
 [100 110 121]]
[[ 24  44  66]
 [ 90 110 132]]

Анализ данных С помощью Pandas

Python Pandas используется для реляционных или помеченных данных и предоставляет различные структуры данных для манипулирования такими данными и временными рядами. Эта библиотека построена поверх библиотеки NumPy. Этот модуль обычно импортируется как:

import pandas as pd

Здесь pd упоминается как псевдоним Pandas. Однако нет необходимости импортировать библиотеку, используя псевдоним, это просто помогает писать меньший объем кода при каждом вызове метода или свойства. Pandas обычно предоставляют две структуры данных для манипулирования данными, это:

• Серии
• Фрейм данных

Серии:

Серия Pandas представляет собой одномерный помеченный массив, способный содержать данные любого типа (integer, string, float, объекты python и т.д.). Метки оси в совокупности называются индексами. Серия Pandas - это не что иное, как столбец на листе Excel. Метки не обязательно должны быть уникальными, но должны иметь хэшируемый тип. Объект поддерживает индексацию как на основе целых чисел, так и на основе меток и предоставляет множество методов для выполнения операций с индексом.

Серия создания Python Pandas

import pandas as pd
import numpy as np

# Creating empty series
ser = pd.Series()

print(ser)

# simple array
data = np.array(['g', 'e', 'e', 'k', 's'])

ser = pd.Series(data)
print(ser)

Вывод:

Series([], dtype: object)
0    g
1    e
2    e
3    k
4    s
dtype: object

Фрейм данных:

Pandas DataFrame — это двумерная изменяемая по размеру, потенциально неоднородная табличная структура данных с маркированными осями (строками и столбцами). Фрейм данных — это двумерная структура данных, то есть данные расположены в виде таблицы по строкам и столбцам. Pandas DataFrame состоит из трёх основных компонентов: данных, строк и столбцов.

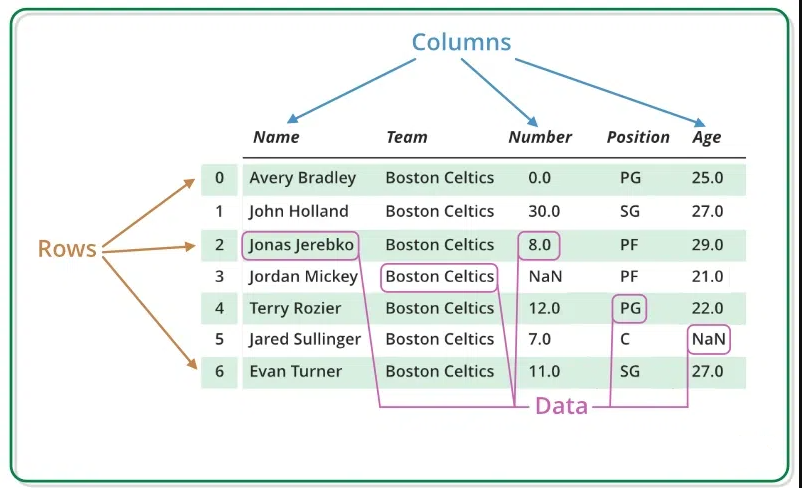
Его можно создать с помощью метода Dataframe() и, как и серию, он может состоять из данных разных типов и структур.

Python Pandas Создает фрейм данных

import pandas as pd

# Calling DataFrame constructor
df = pd.DataFrame()
print(df)

# list of strings
lst = ['G', 'F', 'G', 'i',
            'p', 'f', 'G']

# Calling DataFrame constructor on list
df = pd.DataFrame(lst)
df

Вывод:

Empty DataFrame
Columns: []
Index: []

Создание фрейма данных из CSV

Мы можем создать фрейм данных из CSV-файлов с помощью функции read_csv().

Python Pandas читают CSV

import pandas as pd

# Reading the CSV file
df = pd.read_csv("Iris.csv")

# Printing top 5 rows
df.head()

Вывод: